どうも、とがみんです。
以前の記事で、ディープラーニングの起源となるパーセプトロンについて紹介しました。
この記事では、パーセプトロンで構成されるニューラルネットワークとその仕組みについてまとめていきます。
この記事では、パーセプトロンで構成されるニューラルネットワークとその仕組みについてまとめていきます。
Contents
ニューラルネットワークとは?
ニューラルネットワークとは、人間の脳神経系のニューロンをモデル化したものを組み合わせたもののことを言います。
パーセプトロンをネットワークのように網状に組み合わせたシステムをいいます。
以下の図はニューラルネットワークの一例です。


以前の記事で、パーセプトロンの重みや閾値を定めることによって、ANDゲートについて考えました。
パーセプトロンを多層化することによって、より複雑な関数を表現することができるようになるので、複雑な分類が可能になります。
反面、ANDゲートのような単純なものを作る場合、重みを決定する作業は簡単でしが、
多層化することによって、重みパラメータを決定する作業が大変になってしまいます。
しかし、ニューラルネットワークには、学習データから重みパラメータを自動で決定していく機能があります。
次に、ニューラルネットワークの仕組みについてまとめていきます。
ニューラルネットワークの仕組み
ニューラルネットワークは、パーセプトロンの組み合わせであり、その活性化関数には、ステップ関数ではなく、シグモイド関数が用いられます。
また出力層の活性化関数には、恒等関数、分類問題ではソフトマックス関数が用いられます。
ステップ関数とシグモイド関数
パーセプトロンには、活性化関数として、ステップ関数が用いられていましたが、ニューラルネットワークにはシグモイド関数が使われています。
以下が、それぞれのグラフを比較したものです。
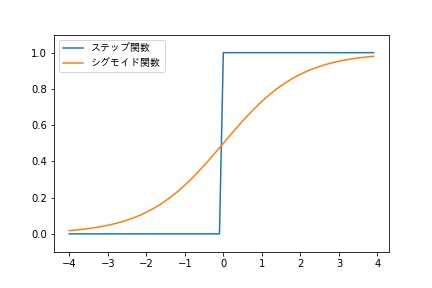

ステップ関数
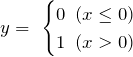
シグモイド関数
![]()
シグモイド関数は、ステップ関数と比べ、滑らかな曲線であり、入力に対して、連続的に出力が変化します。
この性質は、ニューラルネットワークの「学習」において重要な性質になります。
恒等関数とソフトマックス関数
出力層においては、恒等関数、または、ソフトマックス関数を用います。
恒等関数は、出力層の直前から送られてきた値をそのまま出力する関数で、データから値を予測する回帰問題で使用します。
ソフトマックス関数は、データを分類する問題で使用し、最終的な合計値が1となるように算出することが特徴です。
そのため、出力結果を確率として捉えることが可能です。
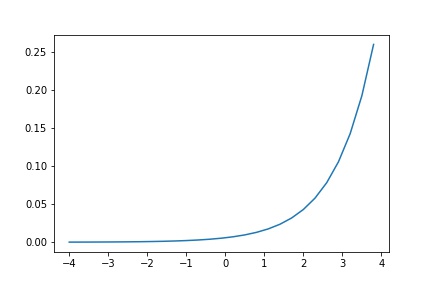

ソフトマックス関数
![]()
下図では、入力したものが「0」、「1」、「2」のどれであるのかを分類するニューラルネットワークの一例で、ソフトマックス関数を通すことで、全ての出力の和が1になります。
なので、出力を確率とみなすことができ、入力したデータが「1」である可能性が70%というような捉え方ができます。
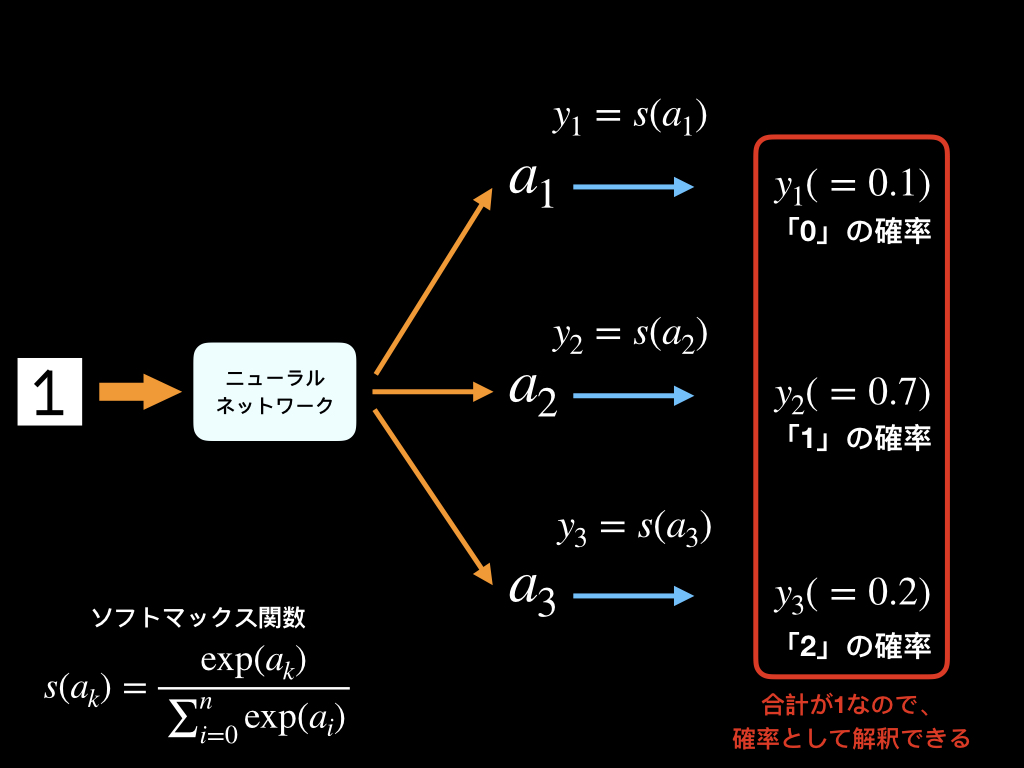

ニューラルネットワークによる機械学習のイメージ
データの入力から出力まで
ニューラルネットワークで、分類問題を解く場合は、入力層はデータの次元数に合わせ、
出力層は分類したい種類、クラスと同じユニットで構成します。
8ピクセル×8ピクセルの「0」〜「9」が描かれた画像を分類したい場合は、入力数64の出力数10といった感じです。
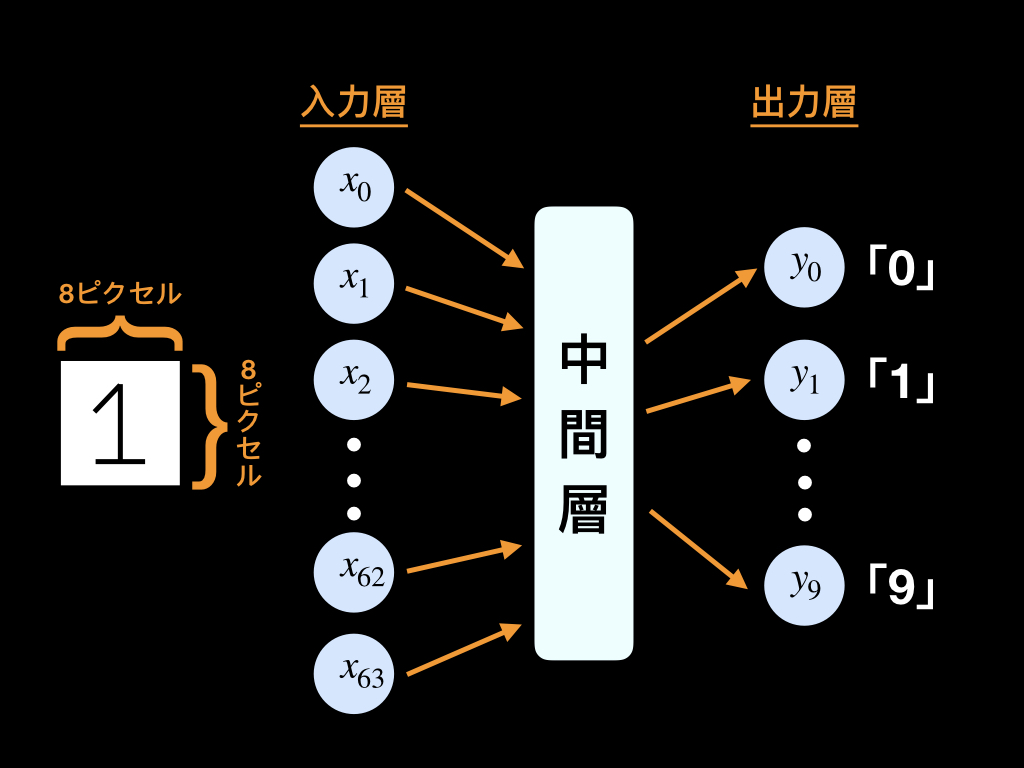

ニューラルネットワークの学習のイメージ
ニューラルネットワークにおける学習とは、入力データに対する出力結果が適切になるように、重みパラメータやバイアスを変化させていくことです。
出力結果と正解データの差分が小さくなるように、重みパラメータやバイアスを定めて行きます。
どのように学習させていくのかの具体的な説明は以下の記事で紹介しています。
まとめ
ニューラルネットワークの仕組みについて説明しました。
機械学習の仕組みに対するイメージがついたでしょうか?
学習の方法、重みの決め方等今後書いて行く予定です。














