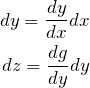どうも、とがみんです。
以前の記事で、ニューラルネットワークがどういうものなのか、また、学習のイメージについて紹介しました。
この記事では、ニューラルネットワークの学習について、誤差逆伝播法等、具体的な仕組みについて紹介していきます。
Contents
ニューラルネットワークの学習とは?
ニューラルネットワークにおける学習とは、訓練用のデータから、最適な重みのパラメータを定めることです。
以下の記事でANDゲートを作るにあたって、条件を満たす重みパラメータや閾値(バイアス)を定めました。
しかし、画像分類等、より複雑な処理を行うニューラルネットワークでは、パラメータの個数が膨大になり、
適切な重みパラメータやバイアスの値を手作業で定めることは、ほぼ不可能になります。
なので、訓練用のデータを用意し、そのデータを用いて学習させることで、自動的に適切なパラメータが定まるようにします。
どのように学習させるのか
ニューラルネットワークの学習には、主に以下の3ステップがあります。
- 学習用データをニューラルネットワークに入力する。
- 出力結果と教師データから損失関数を求める。
- 損失関数が小さくなるように、誤差逆伝播法によって、各パラメータを更新する。
各学習データに対して、上記ステップを繰り返していくことによって、適切な重みパラメータを求めていきます。
学習用データをニューラルネットワークに入力
各重みパラメータをランダムに設定し、学習用データの中から、ランダムにデータを選び出し、学習用データを入力します。
出力と教師データから損失関数を求める
データを入力すると、出力が得られます。そして、出力結果と教師データから損失関数を求めます。
損失関数とは、ニューラルネットワークの性能の悪さを表す指標であり、教師データとどれだけ適合していないかを表します。
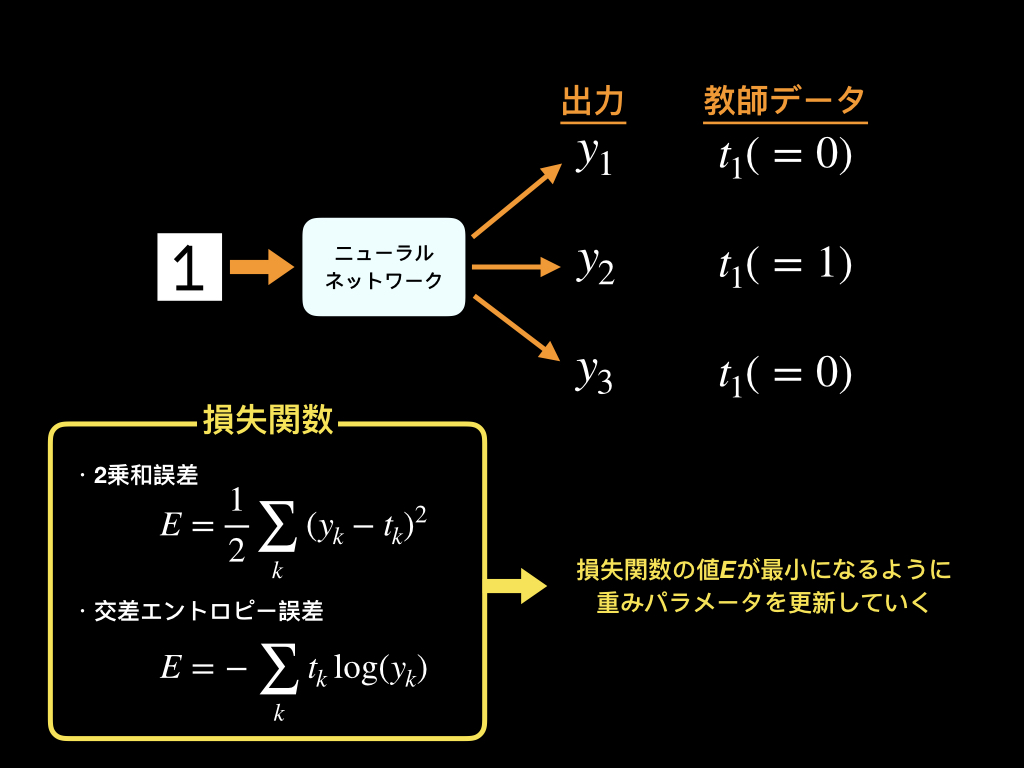
損失関数は主に「2乗和誤差」と「交差エントロピー誤差」があります。
これらの値が小さくなるような重みパラメータを探し出し、更新していきます。
損失関数を各重みパラメータに関して偏微分し、その値が正なら、重みパラメータの値が小さくなる方向に、負なら大きくなる方向に値を更新します。
ηはどれぐらい学習させるかのパラメータです。
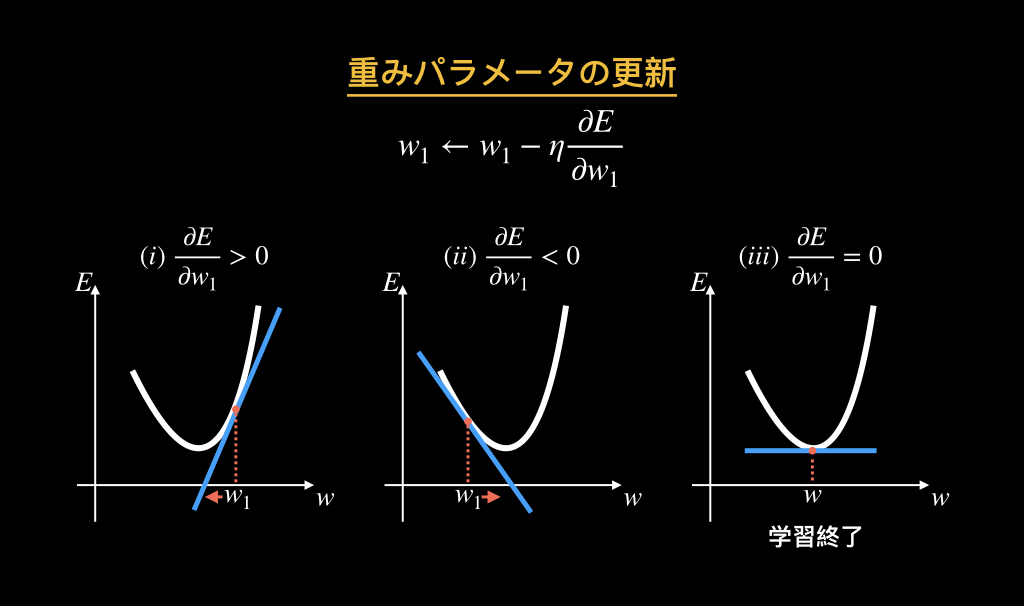
ニューラルネットワークでは、誤差逆伝播法によって、損失関数の値を小さくするような重みパラメータを更新し探していきます。
誤差逆伝播法によるパラメータの更新
誤差逆伝播法とは、重みパラメータにおける損失関数の勾配を求め、重みパラメータを更新を効率良く行うための手法です。
この誤差逆伝播法を理解するにあたって、まず、連鎖律について紹介します。
連鎖律
連鎖律とは、複数の関数によって構成される関数の微分は、それぞれの関数の微分の積によって表すことができるといった性質のことです。
以下の2つの関数があったとします。
yは変数xの関数であり、zは変数yの関数です。それぞれの変数の微小変化による関数の値の微小変化は以下のように表せます。
以上から、関数zの、変数xの微小変化に対する値の変化は、以下のように表せます。
この結果から、関数zのxに対する微分は以下のように表され、それぞれの関数の微分の積によって表されます。これが連鎖律です。
誤差逆伝播法
誤差逆伝播法による、重みパラメータの更新について説明していきます。
誤差伝播法は、重みを更新する際にする損失関数の各パラメータに対して行う勾配を求める計算を効率化する手法です。
以下の図の単純なニューラルネットワークを例に説明していきます。
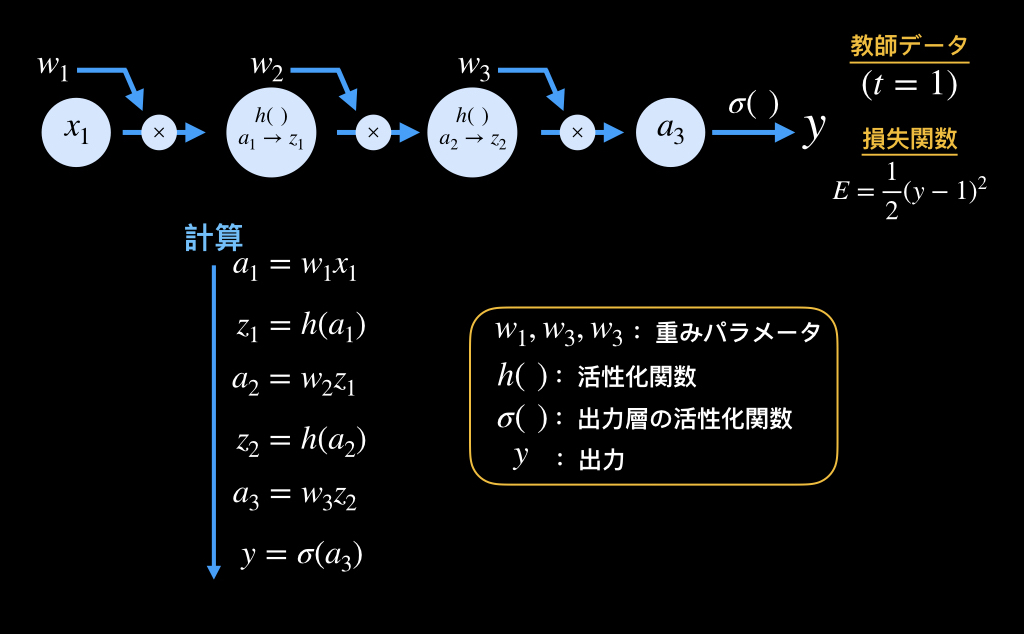
各重みパラメータに関する損失関数の勾配を、連鎖律を利用して求めると以下のようになります。

赤枠で囲った「A」の部分や、緑枠で囲った「B」の部分が共通していることがわかります。
各パラメータにおける損失関数の勾配をそれぞれ求めていった場合、同じ計算を何度もしてしまうため、非効率になってしまいます。
誤差逆伝播法は、何度も同じ計算をしなくて済むような仕組みになっているので、計算量を大幅に減らすことができます。
誤差逆伝播に関する図が以下です。
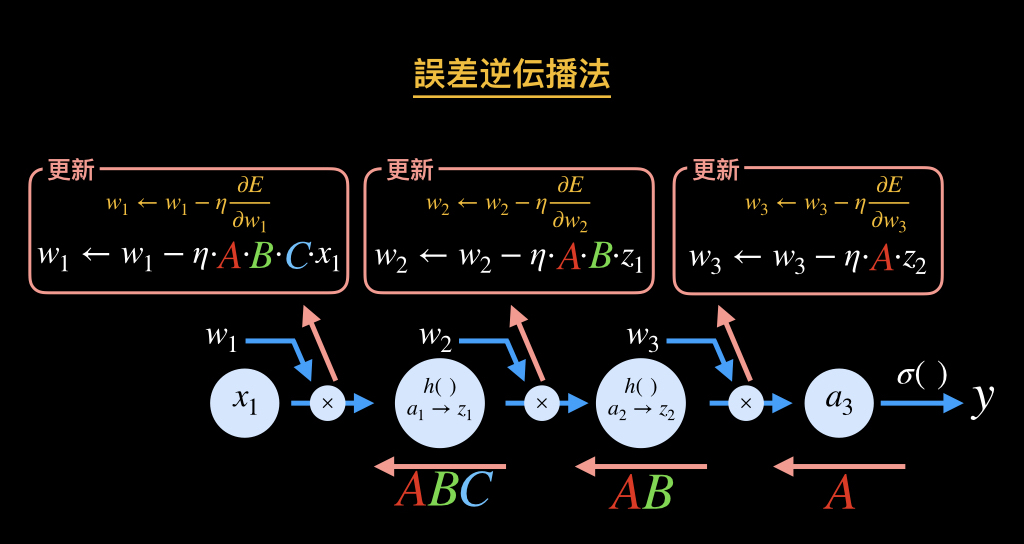
上図のように、出力から入力側に向かって順に学習パラメータを更新していくことから、誤差逆伝播法と呼ばれ、各パラメータの偏微分の計算を効率化します。
このようにして、学習と誤差逆伝播法による、重みパラメータの更新操作を繰り返すことによって、最適な重みパラメータを定めていきます。
まとめ
ニューラルネットワークの学習について、誤差逆伝播法等、具体的な仕組みについて紹介しました。