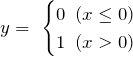人工知能(AI)

【人工知能】活性化関数の種類と使い分け・選び方についてまとめる

  /

どうも、人工知能勉強中のとがみんです。

よりモデルの精度が高いニューラルネットワークを構築するにあたって、どの活性化関数を使用しようかと選び方に迷うことがあるのではないでしょうか？

また、活性化関数の種類が多くて、どういうケースでどの活性化関数を使うのか疑問に思うこともあるのではないでしょうか？

この記事では、ニューラルネットワークで使われる活性化関数にはどのような種類があるのか、精度の高いモデルを作るために、それぞれの活性化関数のメリットデメリットを元に使い分け・選び方についてまとめていきます。

活性化関数とその役割とは?

活性化関数とは、ニューラルネットワークにおいて、入力信号の総和を出力信号に変換する関数のことを言います。

人間における生体ニューラルネットワークでは、ニューロンに対する入力電気信号が「活性化」することによって、次のニューロンへと伝播していくことになりますが、そのどう「活性化するか」を定義したものが活性化関数にあたるものです。

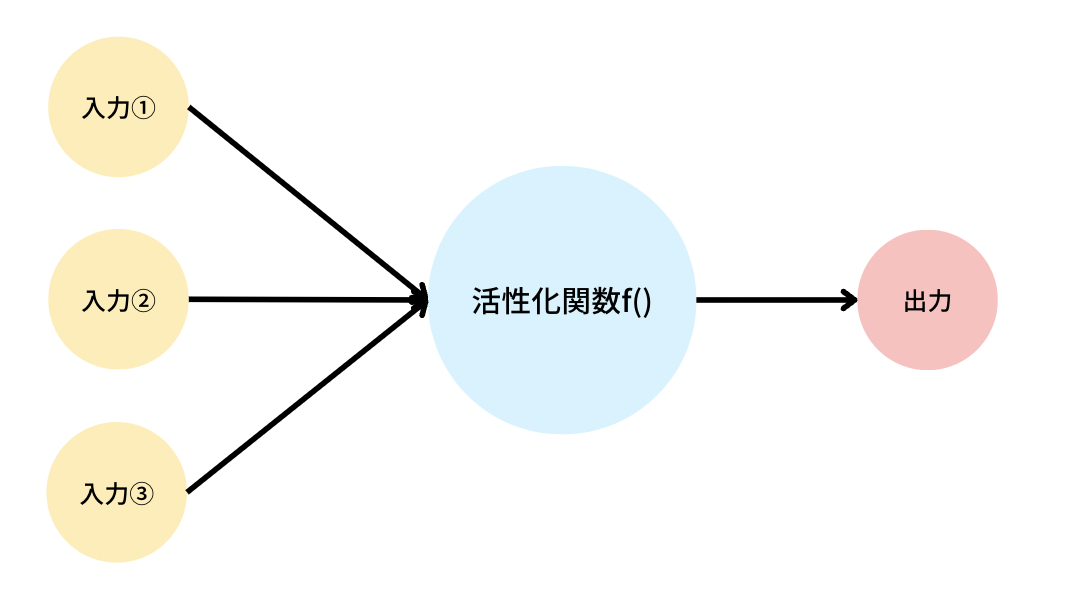
ニューラルネットワークでは、この活性化関数を工夫することによって、複雑な分類問題を解くことができ、

勾配の発散・消失問題を防いだり、学習効率をあげるといった、機械学習におけるモデルの精度を向上させるために、あらゆる種類の活性化関数が考えられてきています。

次にニューラルネットワークに使われている活性化関数の種類や使い分け、選び方等をまとめていきます。

ニューラルネットワークの仕組みにや活性化関数がどのように使われるのか？が気になる場合は、下記の記事に整理しているので、参考にしてください。



活性化関数の種類(中間層)

ステップ関数

ステップ関数は、入力が0を超えたら1を出力し、それ以外は0を出力する関数です。

    $$ y= \ \begin{cases} 0 \,\,\,(x\leq0) \\ 1\,\,\,(x>0) \end{cases} $$

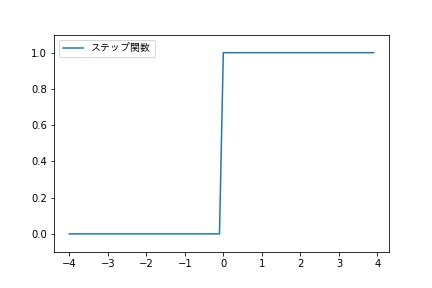
このステップ関数はパーセプトロンの実装で使用されます。

ステップ関数は、x=0以外の点で、その微分が0になるため、誤差逆伝播によるパラーメーターの最適化を行うことができず、ニューラルネットワークを用いたモデルには使われません。


シグモイド関数

シグモイド関数は、入力した値が大きいほど1に近づき、入力した値が小さいほど0に近づく関数です。

    $$ y = \frac{1}{1+\exp(-x)} $$

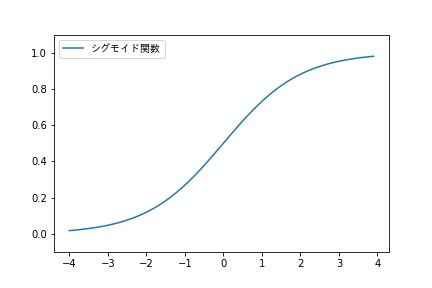
シグモイド関数は、入力に対して連続的に出力が変化し、微分の計算が簡単であることから、

1986年に発表された誤差逆伝播法による学習を伴うニューラルネットワークに使われるようになりました。

シグモイド関数の微分は以下のように表され、ステップ関数とは違い、その微分がゼロにはならないため、誤差逆伝播法による重みパラメータの最適化を行うことができます。

    $$ y^{'} = (1-y)y $$

しかし、このシグモイド関数には、以下のようなデメリットがあります。

  • 入力が極限に大きく、または小さくなると勾配が消える。
  • 誤差逆伝播によるパラメータの更新において、入力層に近ずくほど、学習量が小さくなり、学習が進まなくなってしまう。
  • 微分値の最大値が0.25であり、学習の収束が遅い。

＞Activation functions and it’s types-Which is better?

＞Yann LeCun, Leon Bottou, Genevieve B. Orr, and Klaus-Robert Muller “Efficient BackProp” (1998)

tanh関数

1990年に、活性化関数tanh関数は上記のシグモイド関数のデメリットを改善する活性化関数として提案されました。

    $$ y = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)} $$

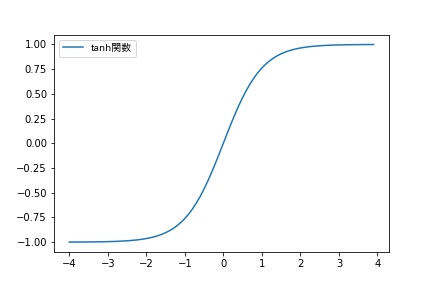
シグモイド関数と比較して、以下のようなメリットがありますが、大きな入力に対する勾配の消失のデメリットがまだ残っています。

メリット

  • 誤差逆伝播法によるパラメータの更新において、微分値の最大値が「1」なので、シグモイド関数に比べ、入力層に近づくにつれて学習が進まなくなってしまう影響が小さい。
  • 出力が−１から１であり、出力がゼロにセンタリングされることで、学習の収束がシグモイド関数よりも容易。

デメリット

  • シグモイド関数同様、入力が極限に大きく(小さく)なると勾配が消えてしまう。

ReLU関数

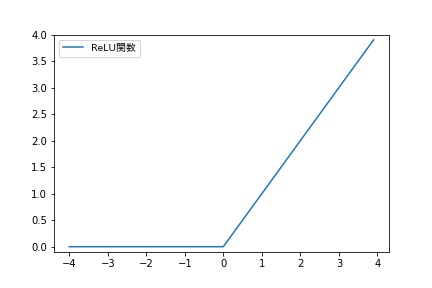
ReLU関数は入力が0を超えていれば、そのまま値を出力し、そうでなければ0を出力するというものです。

    $$ y = max(0,x) $$

ReLU関数はx=0において、非連続で微分不可能ですが、その他の領域では微分可能なので、微分可能な活性化関数として扱われることが多いです。

2011年に、Xavier Glorotらが、中間層(隠れ層)の活性化関数として、ReLU関数を使った方がtanh関数を使うよりも、学習性能がよくなることを発表しています。

＞Deep Sparse Rectifier Neural Networks

ReLU関数は以下のようなメリット、デメリットがあります。

メリット

  • 微分値が定数なので、計算量を圧倒的に減らせ、誤差逆伝播の計算効率が良い。
  • 微分値が一定であることから、誤差逆伝播による勾配の消失問題を防ぐことができる。

デメリット

  • 入力が負の時、微分値が0なので、重みパラメーたの更新がされない。

このようなメリットから、深い層のニューラルネットワークの学習が可能になり、現在多くのニューラルネットワークで使用されている活性化関数です。

また、このデメリットを改善するために、Leaky Relu 、PReLU、Eluなどの様々な活性化関数が提案されています。

＞活性化関数ReLUについてとReLU一族【追記あり】

Leaky Relu

Leaky Relu関数は、ReLU関数の負の入力値における勾配消失を防ぐために、x<0において小さな傾きを持たせた関数です。

    $$ y= \ \begin{cases} x\ (x>0)\ \\ 0.01x\ (x\leq0) \end{cases} $$

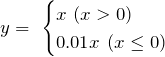
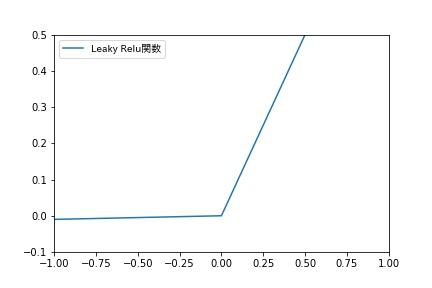
Wikipediaによると、この関数の命名者は、この活性化関数を使う意味はなかったと報告しているそうです。

＞活性化関数｜Wikipedia

PReLU(Parametric ReLU)

PReLUは、ReLUのx<0における傾きを学習させながら適切に変化させます。

    $$ y= \ \begin{cases} x\ (x>0)\ \\ ax\ (x\leq0) \end{cases} $$

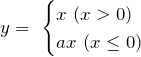
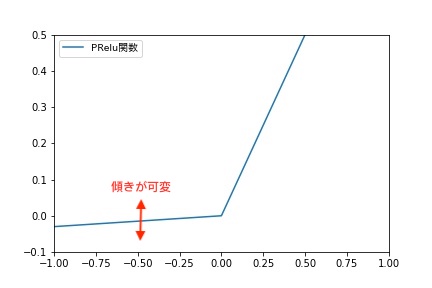
以下の論文では、ReLUと比較して、ほとんど計算量コストをかけずに、性能が改善されたことが報告されています。

＞Delving Deep into Rectifiers:
Surpassing Human-Level Performance on ImageNet Classification

RReLU(Randomized ReLU)

RReLUは学習時に、x<0における傾きを与えられた範囲内でランダムに変化させることによって、過学習を防ぐことができます。

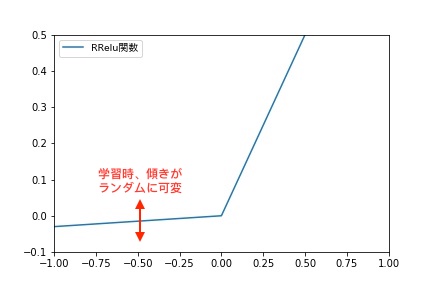
以下の論文で、ReLU関数、Leakey ReLU関数、PReLU関数、RReLU関数の比較がされています。

＞Empirical Evaluation of Rectified Activations in Convolution
Network

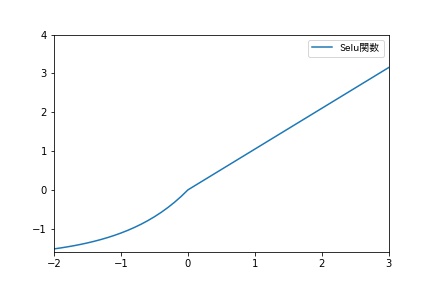
Selu(Scaled Exponential Liner Units)

SELUは以下の式で表される関数です。

    $$ y= \lambda \ \begin{cases} x\ (x>0)\ \\ \alpha(\exp(x)-1)\ (x\leq0) \end{cases} $$

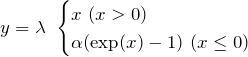
適切なパラメータは理論的に定まり、α=1.67326…、λ=1.0507…となります。

＞ReNom 内にある活性化関数

＞Günter Klambauer, Thomas Unterthiner, Andreas Mayr, Sepp Hochreiter. Self-Normalizing Neural Networks. Learning (cs.LG); Machine Learning

＞[DL輪読会]Self-Normalizing Neural Networks

Elu(Exponential Linear Units)

Seluにおいてλ=1とおいたものがEluです。

    $$ y= \ \begin{cases} x\ (x>0)\ \\ \alpha(\exp(x)-1)\ (x\leq0) \end{cases} $$

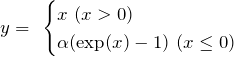
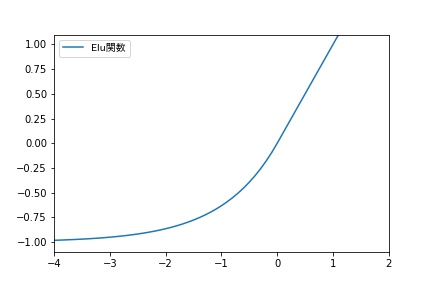
下記の論文ではReLU関数、Leaky ReLU関数、SReLU関数、Elu関数が比較されています。

＞FAST AND ACCURATE DEEP NETWORK LEARNING BY
EXPONENTIAL LINEAR UNITS (ELUS)

Maxout

Maxout関数は、活性化関数自体を学習させるという手法です。

ReLU関数や2次関数など様々な関数に近似することができため、MaxoutはReLUよりも表現力が高く、勾配が消えないという特徴を持っています。

詳しくは以下の記事に書かれています。

＞数式で書き下す Maxout Networks

＞文書分類をタスクとしたPylearn2 の Maxout+Dropout の利用

＞Maxout Network

活性化関数(出力層)

出力層の活性化関数は、中間層の活性化関数とは区別して設計され、誤差関数はその中間層の活性化関数とセットで設計されます。Nは訓練データの個数、tは教師データ、yは出力データです。

恒等関数

回帰分析にニューラルネットワークを使用する場合は、恒等関数を使用します。

    $$ y = x $$

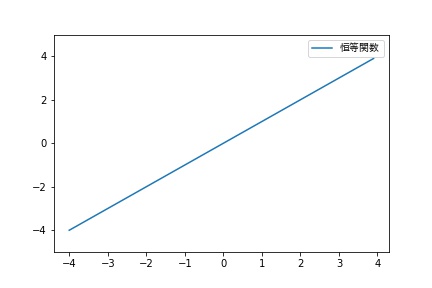
出力層の活性化関数として、恒等関数を使用した場合、誤差関数は、二乗和誤差を利用します。

    $$ E = \frac{1}{2} \sum_{n=1}^{N}(y_n-t_n)^2 $$

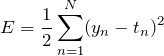
シグモイド関数

二値分類をするニューラルネットワークの出力層の活性化関数として、シグモイド関数を使用します。

    $$ y = \frac{1}{1+\exp(-x)} $$

出力層にシグモイド関数を使用した場合に利用する誤差関数は、以下のものです。

    $$ E = -\sum_{n=1}^{N}(t_n　\log　y_n+(1-t_n)\log(1-y_n)) $$

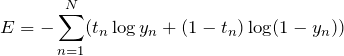
ソフトマックス関数

多クラス分類をするニューラルネットワークにおいては、出力層の活性化関数として、ソフトマックス関数を使用します。

Kは分類するクラスの数です。

    $$ y(x_k) = \frac{\exp(x_k)}{\sum_{i=1}^{K}exp(x_i)} $$

出力の総和が1となり、出力を確率として解釈することができます。

誤差関数には交差エントロピー誤差関数を使用し、偏微分は以下のようになります。

    $$ E = -\sum_{n=1}^{N}\sum_{k=1}^{K}t_{n,k}log y_{n,k}} $$

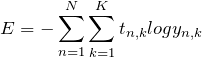
ニューラルネットワークにおける活性化関数の使い分け・選び方

活性化関数の使い分け・選び方に関しては、中間層と出力層で分けて考えられます。

中間層で活用する活性化関数を選ぶ上での観点としては「学習効率が大きいか」「勾配消失問題を防げるか」「過学習が防げるか」という観点でReLU関数やそれから派生された関数が研究され使われることが多いようです。

出力層で活用する活性化関数に関しては、どんな分類問題を解きたいかに依存し、回帰分析をしたい場合は「恒等関数」、二値分類をする場合は「シグモイド関数」、多クラス分類をするニューラルネットワークにおいては、ソフトマックス関数を使用します。

まとめ

活性化関数の種類と使い分け・選び方についてまとめてきました。

ニューラルネットワークに使われる活性化関数としては、「学習効率が大きいか」「勾配消失問題を防げるか」「過学習が防げるか」という観点で、ReLU関数がメジャーだそうですが、ReLU関数をベースにより精度が高く高効率な活性化関数が研究されているようです。

活性化関数の使い分けや選び方を考える上での参考になれば幸いです。

参考文献

活性化関数の紹介

＞Follow
Visualising Activation Functions in Neural Networks

活性化関数についてのまとめ(ステップ関数・シグモイド・ReLU等々)

Delving Deep into Rectifiers:
Surpassing Human-Level Performance on ImageNet Classification

活性化関数｜Wikipedia

＞Activation functions and it’s types-Which is better?

TensorFlow ライブラリの機械学習処理フローの練習コード集

活性化関数ReLUについてとReLU一族【追記あり】

ニューラルネットワーク 活性化関数
RELATED POST