どうも、とがみんです。
この記事では、機械学習のクラスタリングの手法の一つである、k-means法について紹介します。
Contents [hide]
k平均法(k-means)クラスタリングとは
k平均法(k-means法)は、決められたクラスタ数に従って、近い属性、類似度の高い属性のデータを分類するクラスタリングのアルゴリズムの一つです。
クラスタの数「k」をあらかじめ決めておき、クラスタの平均からの距離の2乗和が最小となるように、クラスタV1〜Vkに分類するというものです。
k平均法のアルゴリズム
k平均法は以下のステップによって行われ、データをクラスタリングします。
- 各データxi(i=1,2,3,4…n)に対してランダムにクラスタを割り振る。
- 割り振ったデータを元に、各クラスタの中心Vj(j=1,2,…k)を計算する。
- 各xiと各Vjの距離を求め、xiを最も近いクラスタに割り当て直す。
- 上記の処理で全てのxiのクラスタの割り当てが変化しなかった場合、処理を終了する。
各データxi(i=1,2,3,4…n)に対してランダムにクラスタを割り振る。
全体を2つのクラスタに分類するとします。全てのデータを「赤」と「青」の2つのクラスタに以下のようにランダムに振り分けます。

割り振ったデータを元に、各クラスタの中心Vj(j=1,2,…k)を計算する。
以下のように、2つのクラスタ「赤」と「青」のそれぞれの中心を計算し、「V1」と「V2」とします。
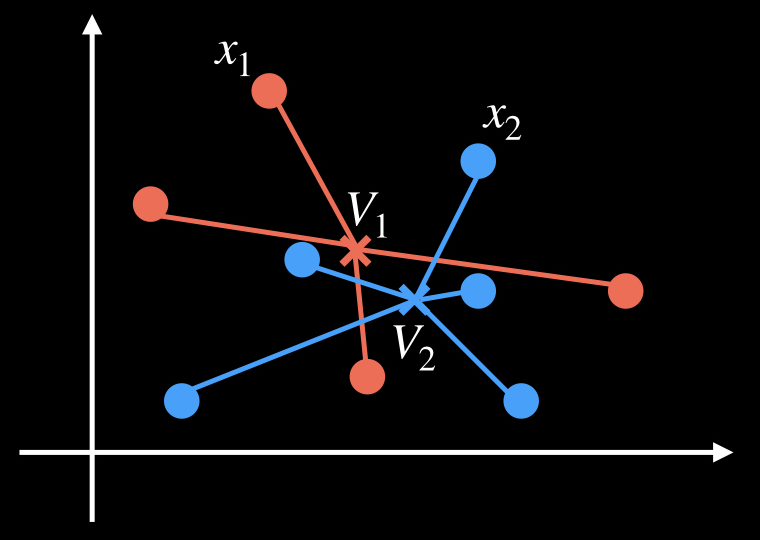
各xiと各Vjの距離を求め、xiを最も近いクラスタに割り当て直す。
各データxiを、近い方のクラスタに割り当て直します。
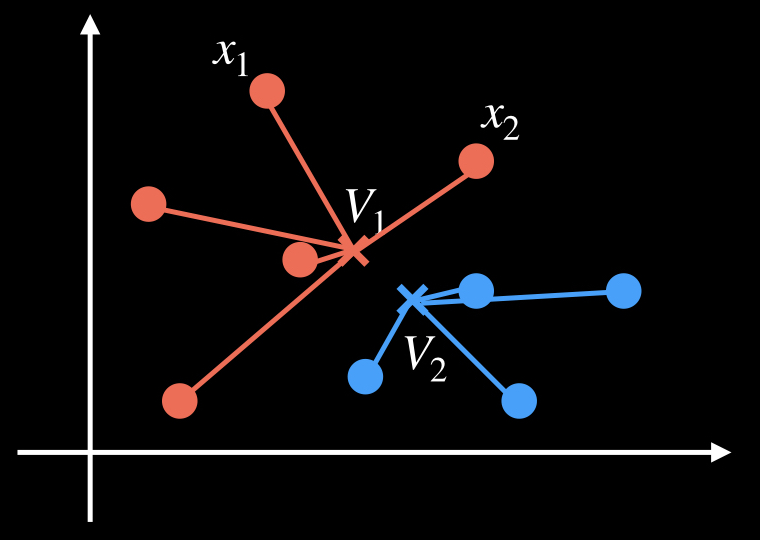
上記の処理で全てのxiのクラスタの割り当てが変化しなかった場合、処理を終了する。
割り当て直した後、クラスタの中心を計算し直します。そして、上記の操作を繰り返していき、クラスタの割り当てに変化がなくなれば、処理を終了します。
このようにして、あらかじめ決めたクラスタの数にデータを分類していきます。
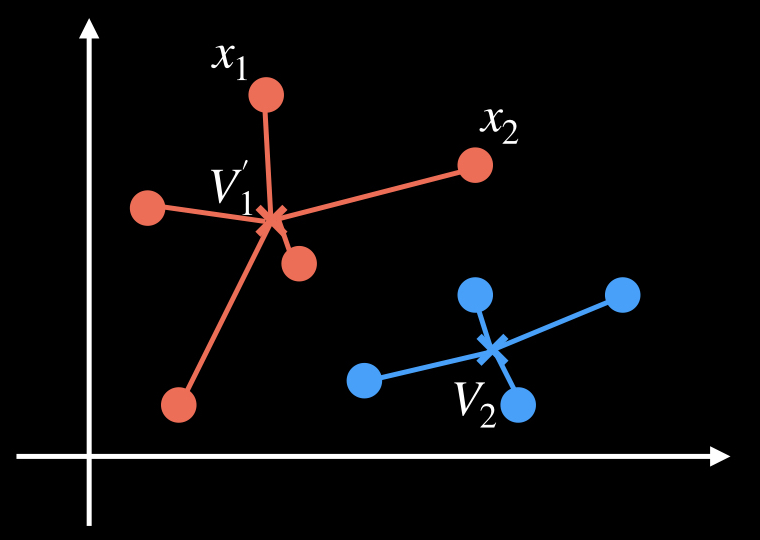
k平均法(k-means)のメリットデメリット
k平均法(k-means)のメリット、デメリットについてです。
メリット
- アルゴリズムが単純
デメリット
- 最初のクラスターをランダムに決定するため、実行するごとに結果が変わる。
k平均法の結果は、最初のクラスタのランダムな割り振りに大きく依存するので、
1回の結果で最良のものが得られるとは限らないので、何度か繰り返し行い、
最良の結果を選択する手法や、k-means++法といった、最初のクラスタの中心点の振り方を工夫する手法が使用される。 - クラスターの数がわからない時、適切な値を決める方法論がない。
最適なクラスタ数を選ぶには、他の計算等による考察を必要がある。
k平均法の実用例
どのような場合に、このクラスタリング分析が使われるのかについてです。
よく使われるのは顧客情報を類似度の高い属性別に分類し、ユーザーの特性に合わせた内容のダイレクトメールを配布したりといった場所に利用されます。
まとめ
機械学習のクラスタリングするための手法の一つである、k-means法についてまとめました。













