どうも、とがみんです。
この記事では、ニューラルネットワーク(ディープラーニング)の起源となるアルゴリズムである、パーセプトロンについて紹介していきます。
パーセプトロンとは?
パーセプトロンは、1957年に、心理学者・計算機科学者のローゼンブラットというアメリカの研究者によって考案されたアルゴリズムです。
>The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain
以下がパーセプトロンに関する図です。

【各パラメータ】
x1,x2 : 入力信号
y : 出力信号
w1,w2 : 重み
θ : 閾値、バイアスともいう。
図の◯は「ニューロン」や「ノード」と呼ばれます。
w1、w2は、重みパラメータといい、各入力信号の重要度をコントロールする値として働きます。
θは閾値、またはバイアスとも呼ばれ、発火のしやすさ、すなわち「1」の出力のされやすさを制御します。
入力信号には、それぞれ重みが乗算され、それらの総和が閾値以下の場合、「0」を出力し、
閾値以上の場合、「1」を出力します。
数式で表すと以下のようになります。
パーセプトロンで論理回路を作る
次にパーセプトロンを使って論理回路を作成してみます。
論理回路とは、論理計算を行う回路のことであり、ANDゲート、ORゲート、NOTゲート等ありまが、ここではANDゲートのみ紹介します。
ANDゲート
ANDゲートとは、入出力が以下のようになるものです。
| x1(入力1) | x2(入力2) | y(出力) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
パーセプトロンを用いて、このAND回路を作成する場合、上記表を満たすような(w1,w2,θ)を決めます。
下式に、x1,x2の値を代入し、出力が上記のようになる条件を求めます。
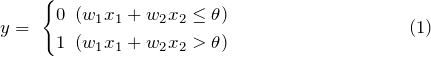
条件は下記のようになります。これを満たすように(w1,w2,θ)を定めればANDゲートができます。
例えば(0.6,0.6,1.0)とかです。

このように、パーセプトロンを用い、重みや閾値を定めることによって回路を作成することができます。
また、このパーセプトロンを多層に組み合わせることによって、複雑な関数であっても表現することができるようになります。
パーセプトロンがどのようにしてディープラーニングに応用されるのか
最後に、このパーセプトロンがどのようにしてディープラーニングに応用されていくのかについて簡単に紹介します。
ディープラーニングでは以下のイメージ図のように、パーセプトロンが多層構造になっています。
多層化することによって、より複雑な関数近似が行えるようになります。
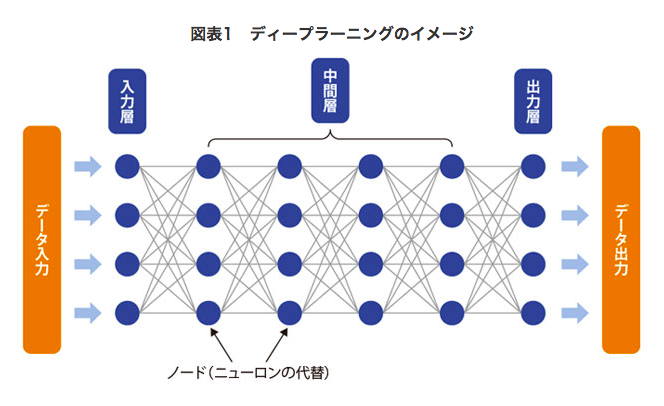

画像引用:「ディープラーニング」など先進AIの活用において、官民一体となった日本の攻勢が始まる!
このように、パーセプトロンはディープラーニングの起源となるアルゴリズムです。
まとめ
ニューラルネットワーク(ディープラーニング)の起源となるアルゴリズムである、パーセプトロンについて紹介しました。















