どうも、とがみんです。
この記事では、データ分析手法の一つである、データの次元圧縮、特徴抽出のための主成分分析(PCA:Principal Components Analysis)について紹介していきます。
Contents
主成分分析とは
主成分分析とは、データの特徴を抽出したり、たくさんの次元(指標)のデータを、データの持つ情報をできる限り損なわずに、より少ない指標に要約するための手法です。
以下のようなデータの分布があった場合、最もデータが散らばっている方向に第一主成分を取り、それと直角に第2主成分軸を取ります。
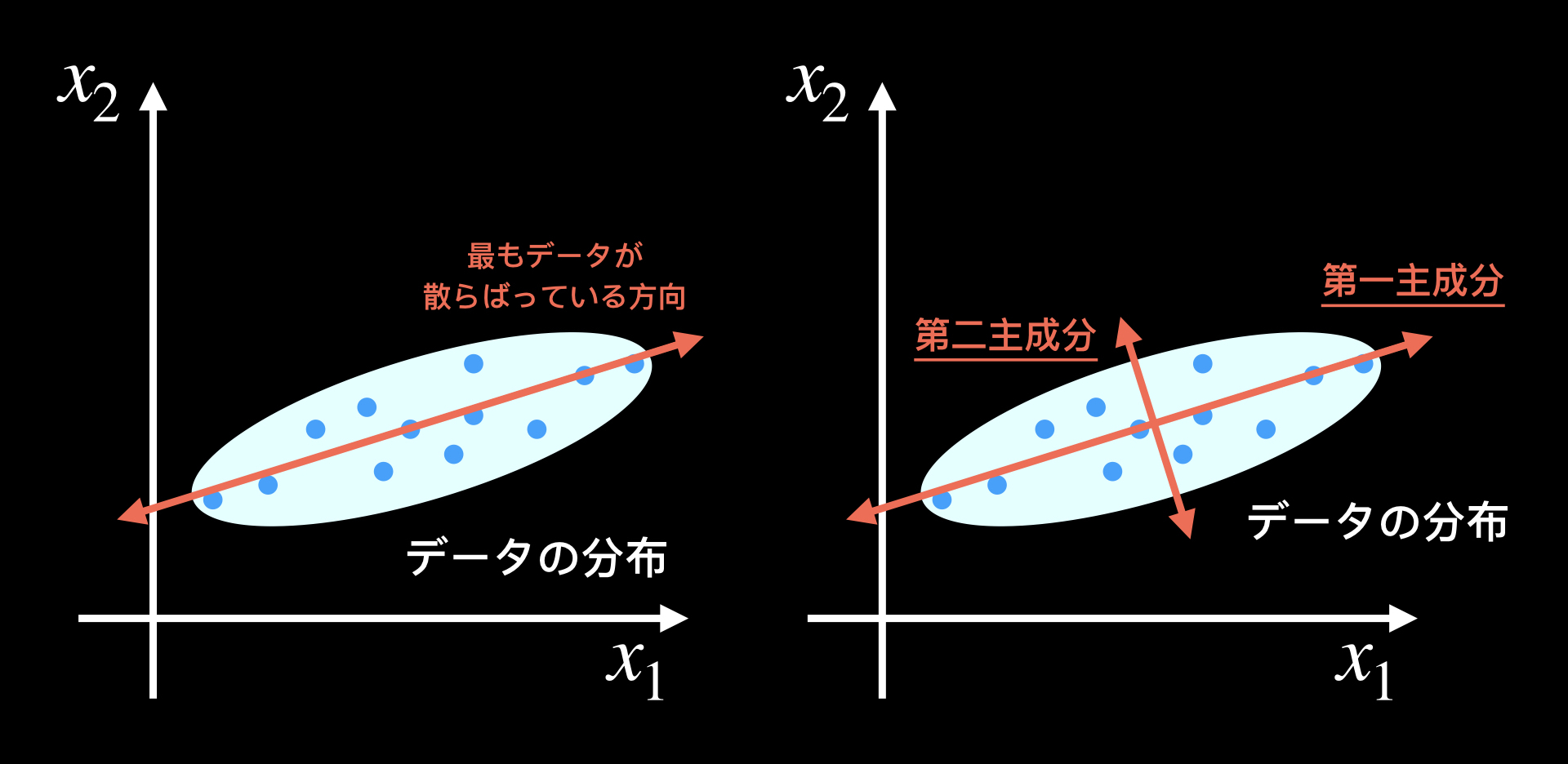
このように、よりデータを表す成分を抽出します。また、多次元データの場合、元データに寄与しない成分を無視することによって、次元の圧縮、削減をすることができます。
主成分分析の目的
主成分分析を行う目的としては主に、以下のようなものがあります。
- データの次元圧縮
- データの特徴を抽出
- 人間が認識しにくい多次元データの視覚化
データの次元圧縮
多次元データにおいて、データのばらつきが少ない部分は、データに共通するパターンなので、あまり意味をなしません。そういった特徴を見つけ、無視することによりデータの次元を圧縮します。
データの特徴を抽出
主成分分析はデータのばらつきが大きい部分に注目するので、よりデータを識別しやすくなります。
多次元データの視覚化
多次元のデータは人間にとって認識することが難しいので、データの次元を圧縮することによって、その特徴を視覚化するのに役立ちます。
次に、具体的な主成分分析のアルゴリズムについて紹介していきます。
主成分分析のアルゴリズムの流れ
実際に主成分分析がどのようなアルゴリズムで行われるかについて以下のステップで紹介していきます。
- データセットから共分散行列Cを求める.
- 共分散行列のCの固有値と固有ベクトルを求め、軸を定める.
- (次元削減)
分散:ある一群のデータの平均値とそれぞれの数値との差の二乗に対する平均値。
共分散:2種類のデータの関係を表す指標。
分散共分散行列:分散の概念を多次元変数に拡張して行列としたもの。
データセットから共分散行列を求める
データセットから共分散行列を求めます。
s11はx1軸方向の分散、s12とs21はx1とx2の共分散です。それらは以下図の分散の式によって計算されます。
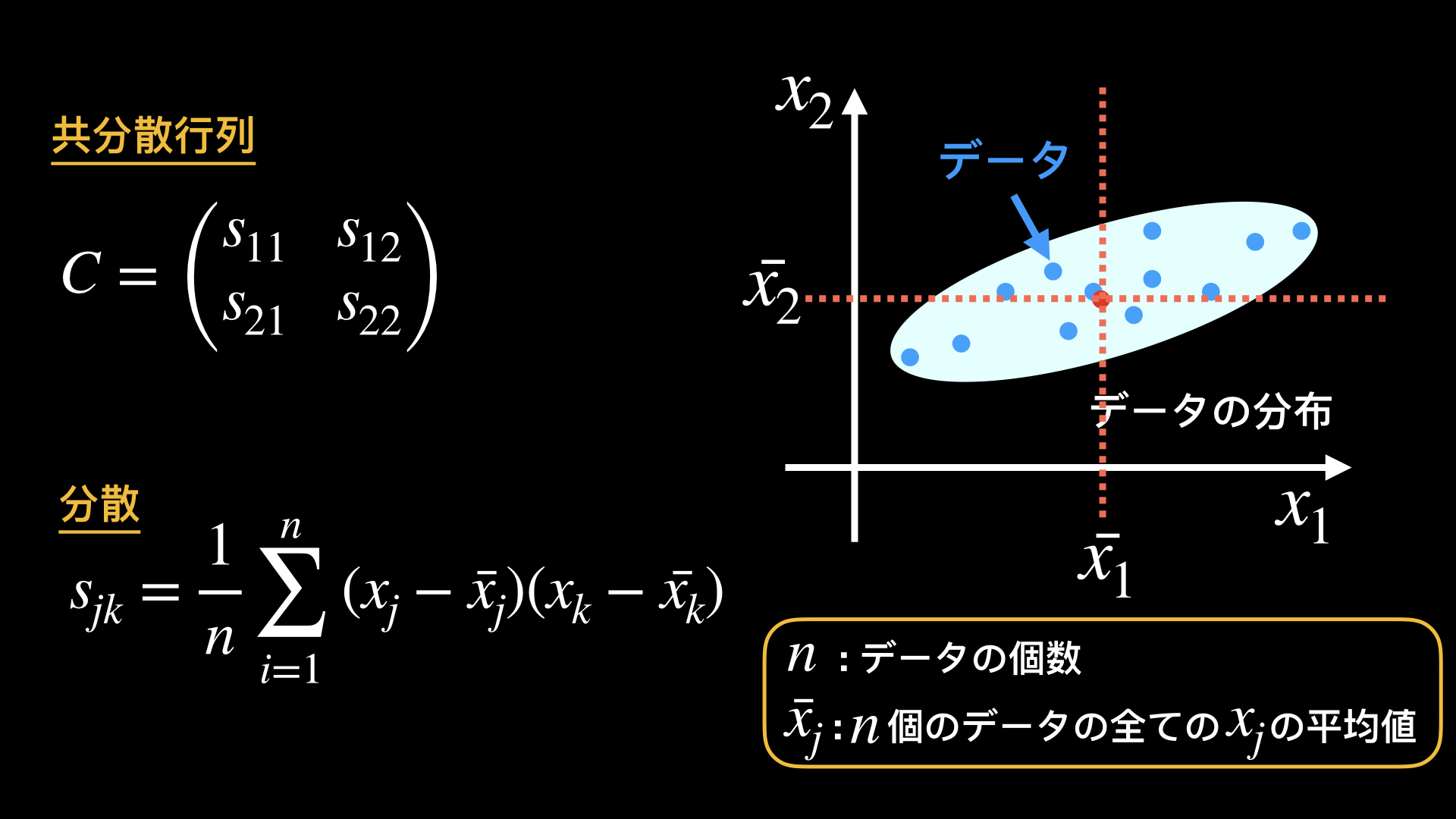
共分散行列のCの固有値と固有ベクトルを求める.
求めた共分散行列の固有値と固有ベクトルを求めます。
固有値固有ベクトルの求め方は以下の記事を参考にしてください。
この固有値が、元の情報をどれだけ保持しているかを表し、固有ベクトルは主成分の軸を表します。
最も大きい固有値に対する固有ベクトルが第一主成分軸となり、2番目に大きい固有値に対する固有ベクトルが、第二主成分軸になります。
このようにして、主成分軸を求めていきます。
次元削減
次元削減は、このようにして求めた軸の中で、最も元のデータに与える影響の少ないものを削除することで次元を削減します。
主成分分析を用いるケース
主成分分析を用いる例として、以下のようなものがあります。
- アンケート調査の結果分析
- 商品評価
- 研究開発
- 画像処理
詳しくは以下の記事を参考にしてください。
まとめ
主成分分析について紹介しました。
参考文献
>https://statistics.co.jp/reference/software_R/statR_9_principal.pdf
>多変 量解析法 の概説,特 に主成分 分析,
重回帰分析,判 別分析 を中心 に して














